Pulleys
Problems involve two weights either side of a pulley. The heavier weight pulls on the lighter causing both to accelerate in one direction with a common acceleration.

calculation of acceleration 'a'

The study of the causes of motion is called dynamics, or mechanics. The relation between force and acceleration was given by Isaac Newton in his three laws of motion, which form the. Over any pulley, the pulley's mass can also be ignored.

calculation of tension 'T'

Example
A 3 kg mass and a 5 kg mass are connected over a pulley by a light inextensible string.
When the masses are released from rest, what is:
i) the acceleration of each mass?
ii) the tension in the string
(Take g=9.8 ms-2 . Answer to 2 d.p.)
i)

ii)

Towe-bar/towe-rope/chains
Usually one body pulled horizontally by another with each linked by a towe-bar or similar. This is similar to the pulley but drawn out in a line.

assuming no friction,

calculation of acceleration 'a'

calculation of tension 'T'

Example
A car of mass 600 kg towes a trailer of mass 250 kg in a straight line using a rigid towe-bar.
The resistive force on the car is 200N.
The resistive force on the trailer is 80N.
If the forward thrust produced by the engine of the car is 800 N, what is(to 3 d.p.)
i) the acceleration of the car
ii) the tension in the towe-bar
i) looking at all the forces on the car and trailer together

ii)

Inclined plane with pulley
The pulley at the end just changes the direction of the force. problems involve the resolved component of the weight of the object down the plane.

for a mass sliding down a smooth incline

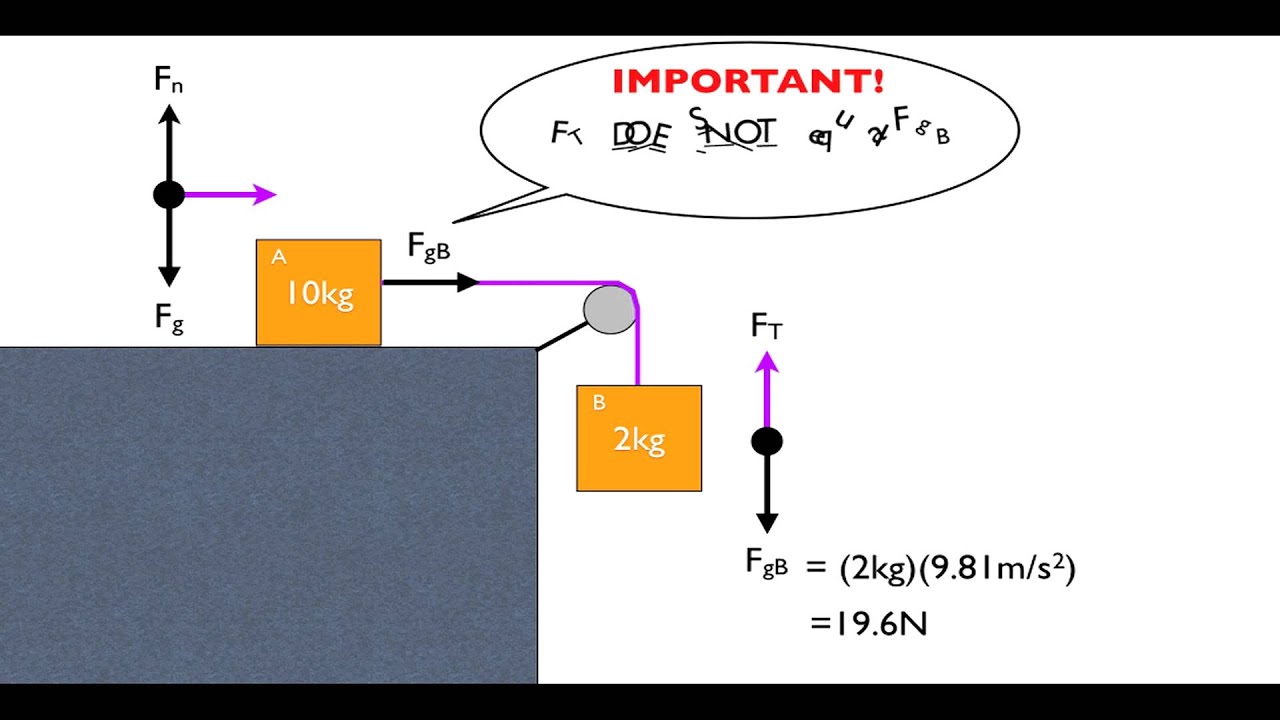
for a mass pulled up an incline via a pulley

Example
A 2 kg mass on a smooth 30o plane is connected to a 5 kg mass by a light inextensible string passing over a pulley at the top of the plane.
When the particles are released from rest the 2 kg mass moves up the plane.
i) what is the acceleration of the 2 kg & 5 kg masses?
ii) What is the tension in the string?

i)

ii)

Mass ascending or descending in a lift

it is important to remember that there are only two forces on the body in the lift - the weight down and the reaction of the floor up.

Example
A person of mass 100 kg stands in a lift.
What is the force exerted by the lift floor on the person when the lift is:
i) moving upwards at 3 ms-1
ii) moving downwards at 4 ms-1

i)

ii)
Draw all the forces which affect the bucket and the block in the picture. Write the force equations for them.
Forces that affect the bucket m2:
(vec{F}_{G_2})…weight
(vec{T})…tension force by which the rope affects the bucket
Forces that affect the block m1:
(vec{F}_{G_1})…weight
(vec{T}prime)…tension force by which the rope affects the block
Problems
(vec{T}primeprime)…tension force by which the rope affects the block
The vector force equation for the bucket:
[vec{F}_{G2}+vec{T}=m_2vec{a}_2tag{1}]
The vector force equation for the block:
[vec{F}_{G1}+vec{T}prime+vec{T}primeprime=m_1vec{a_1}tag{2}]
We choose the y-axis the way it is marked on the picture.
We rewrite equations (1) and (2) to scalar form:
[T-F_{G2}= m_2a_2tag{3}]
[F_{G1}-Tprime-Tprimeprime = m_1a_1tag{4}]
Because we leave the mass of the pulley system and the rope out of account they have no moment of inertia and don’t affect the tension forces. The following holds for the magnitude of the tension forces:
[|vec{T}|=|vec{T}prime|=|vec{T}primeprime|]
We rewrite equations (3) and (4):
[T-F_{G2}= m_2a_2tag{5}]
[F_{G1}-2T= m_1a_1tag{6}]
Relation between the magnitudes of acceleration a1 and a2:
If the bucket goes up a distance s, the block goes down a distance (frac{s}{2}).
[s=frac{1}{2}a_2t^2]
[frac{s}{2}=frac{1}{2}a_1t^2]
We divide the first equation by the second equation, yielding:
[2=frac{a_2}{a_1}]
[a_2=2a_1tag{7}]
Equation (5) and equation (6) can be written as:
[T-m_2g= m_22a_1tag{8}]
[m_1g-2T= m_1a_1tag{9}]
We have two equations (8) and (9) in two variables T and a1. From them we can determine the magnitude of the acceleration a1 and the force T. We multiply equation (8) by 2 and add both equations up:
[m_1g-2m_2g= m_1a_1+4m_2a_1]
[(m_1-2m_2)g= (m_1+4m_2)a_1]
[a_1=frac{(m_1-2m_2)g}{m_1+4m_2}tag{10}]
According to equation (7):
[a_2=2a_1=2frac{(m_1-2m_2)g}{m_1+4m_2}=frac{(2m_1-4m_2)g}{m_1+4m_2}tag{11}]
The magnitude of the tension force T is given for example by equation (8):
[T-m_{2g}= m_22a_1]
[T=m_22a_1+m_{2g}=m_2frac{2(m_1-2m_2)g}{m_1+4m_2}+m_2g]
[T=frac{2(m_2m_1-2m_2^2)g}{m_1+4m_2}+m_2g =frac{(2m_2m_1-4m_2^2+m_2(m_1+4m_2))g}{m_1+4m_2}]
[T=frac{(2m_2m_1-4m_2^2+m_2m_1+4m_2^2)g}{m_1+4m_2}= frac{3m_2m_1g}{m_1+4m_2}]
[T=frac{3m_2m_1g}{m_1+4m_2}tag{12}]